技术分享
图解 Spark GraphX 图计算基于 ConnectedComponents 函数实现连通图底层原理
 按照官网的介绍,NebulaGraph Algorithm 是一款基于 GraphX 的 Spark 应用程序,通过提交 Spark 任务的形式,使用完整的算法工具对 NebulaGraph 数据库中的数据执行图计算。
按照官网的介绍,NebulaGraph Algorithm 是一款基于 GraphX 的 Spark 应用程序,通过提交 Spark 任务的形式,使用完整的算法工具对 NebulaGraph 数据库中的数据执行图计算。
通俗而言,就是基于 NebulaGraph Algorithm,通过配置读取出存储在 NebulaGraph 的数据源,然后转换成 GraphX 图结构(具备顶点和边的数据集),再结合 Spark GraphX 提供的算法,例如 GraphX 的PageRank、ConnectedComponent 等一系列算法函数,进一步去计算出该图里具备一定价值的关联数据。
在 NebulaGraph 社区里有一篇《NebulaGraph 在众安保险的图实践 🔗》的文章,就提到过,在贷前的用户授信申请环节,通过 NebulaGraph 结合 GraphX 的联通分量算法 Connected Component,可提取出一张张关系网,进而计算出每张关系网里各顶点的关联情况。文中提到曾在一张被提取出来的关系网中,计算出一个热点手机号被五六十个其他用户设置为家庭联系人手机号——这样关联数量异常的情况,往往很可能就存在团伙欺诈。
可见,NebulaGraph 结合 GraphX 的联通分量算法 Connected Component,能够实现提取图数据里各个关系网的功能,这具备了一定的风控业务价值。
下面就介绍一下该联通分量算法 Connected Component 的用法及底层实现原理,方便能在熟悉联通算法的基础上,更好地应用在适合的场景里。
联通图说明
连通图是指图中的任意两个顶点之间都存在路径相连而组成的一个子图。
用一个案例来说明,例如,下面这个叫 graph 的大图里,存在两个连通图——
左边是一个连通图,该子图里每个顶点都存在路径相连,包括顶点:{(5L, "Eve"), (7L, "Grace"), (1L, "Alice"), (2L, "Bob"), (3L, "Charlie")}。
右边同样是一个连通图,该子图里每个顶点都存在路径相连,包括顶点:{(8L, "Henry"),(9L, "Ivy"),(6L, "Frank")}。
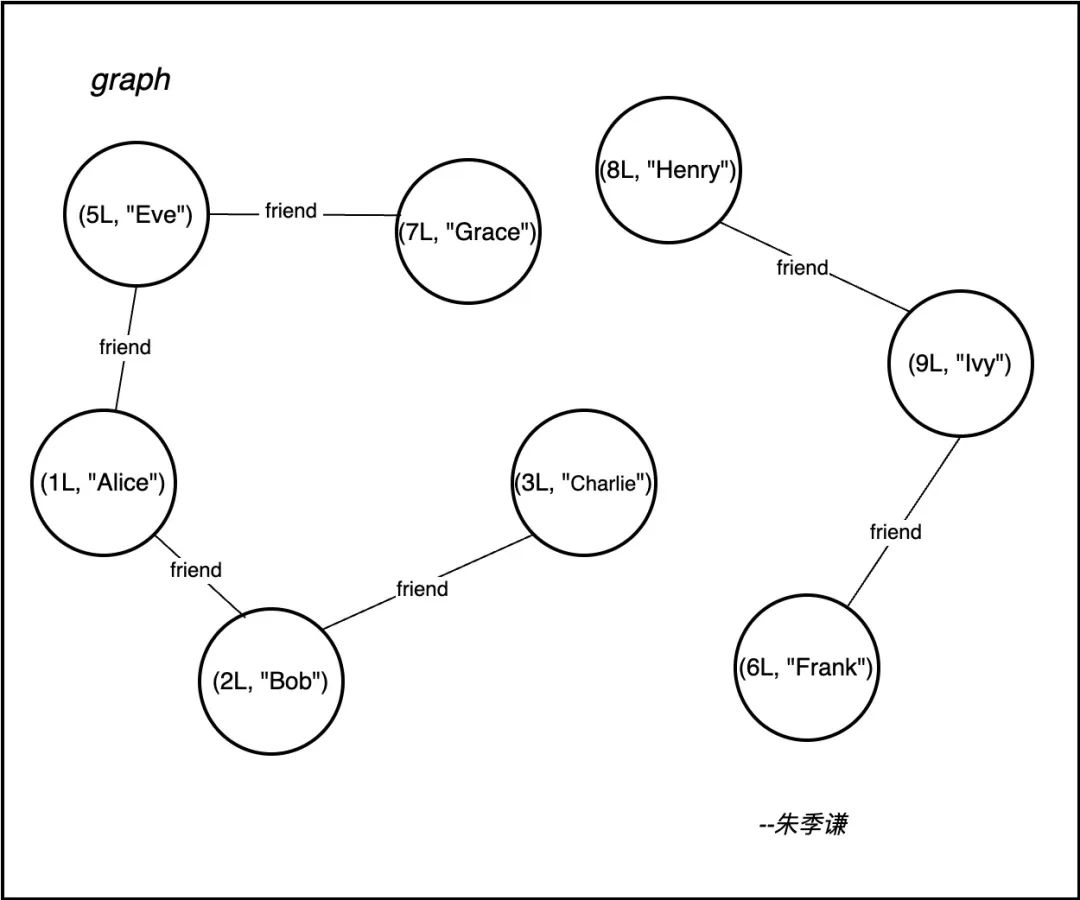
在现实生活里,这两个子图就相当某个社区里两张家庭关系网。
那么,在一个大网里如何得到各个关系网的数据呢?
这时,就可以使用到 Spark GraphX 的 connectedComponents 函数,网上关于它的介绍,基本都是说它是 GraphX 三大图算法之一的联通组件。
通俗解释,就是通过这个联通函数,可以将每个顶点都关联到连通图里的最小顶点,例如,前面提到的子图 {(8L, "Henry"),(9L, "Ivy"),(6L, "Frank")},在通过 connectedComponents 函数处理后,就可以得到每个顶点关联到该子网的最小顶点 ID。该子图里的最小顶点 ID 是 6L,那么可以处理成这样结构的数据——{(8L,6L),(9L,6L),(6L,6L)}。
可以看到,各个顶点都关联到该子网里的最小顶点 6L,这不就意味着,通过该最小顶点 6L,反过来就可以将与 6L 有关联的顶点都查找出来了吗?
这样,通过最小顶点 6L,就能提取出该子网里的顶点集合 {(8L, "Henry"),(9L, "Ivy"),(6L, "Frank")}——这个集合表示一个子网顶点集合。
案例说明
基于以上的图顶点和边数据,创建一个 GraphX 图(在生产环境结合 NebulaGraph 的情况下,这些数据需要从某个数据源读取,这里可以统一从 NebulaGraph 读取)——
`val conf = new SparkConf().setMaster("local[*]").setAppName("graphx")
val ss = SparkSession.builder().config(conf).getOrCreate()
// 创建顶点 RDD
val vertices = ss.sparkContext.parallelize(Seq(
(1L, "Alice"),
(2L, "Bob"),
(3L, "Charlie"),
(5L, "Eve"),
(6L, "Frank"),
(7L, "Grace"),
(8L, "Henry"),
(9L, "Ivy")
))
// 创建边 RDD
val edges = ss.sparkContext.parallelize(Seq(
Edge(5L, 7L, "friend"),
Edge(5L, 1L, "friend"),
Edge(1L, 2L, "friend"),
Edge(2L, 3L, "friend"),
Edge(6L, 9L, "friend"),
Edge(9L, 8L, "friend")
))
//创建一个 Graph 图
val graph = Graph(vertices, edges, null)`
调用图 graph 的 connectedComponents 函数,顺便打印一下效果,可以看到,左边子图 {(5L, "Eve"), (7L, "Grace"), (1L, "Alice"), (2L, "Bob"), (3L, "Charlie")} 里的各个顶点都关联到了最小顶点 1,右边子图 {(8L, "Henry"),(9L, "Ivy"),(6L, "Frank")} 里的各个顶点都关联到了最小顶点 6。
`val cc = graph.connectedComponents()
cc.vertices.foreach(println)
打印的结果——
(2,1)
(6,6)
(7,1)
(1,1)
(9,6)
(8,6)
(3,1)
(5,1)`
注意一点,connectedComponents 是可以传参的,传入的数字,是代表各个顶点最高可以连通迭代到多少步去寻找所在子图里的最小顶点。
举个例子,可能就能明白了,假如,给 connectedComponents 传参为 1,那么代码执行打印后,如下——
`val cc = graph.connectedComponents(1)
cc.vertices.foreach(println)
打印的结果——
(2,1)
(5,1)
(8,8)
(7,5)
(1,1)
(9,6)
(6,6)
(3,2)`
你会发现,各个顶点的联通组件即关联所在子图的最小顶点,大多都变了,这是因为设置参数为 1 后,各个顶点沿着边去迭代寻找联通组件时,只能迭代一步,相当本顶点只能走到一度邻居顶点,然后将本顶点和邻居顶点比较,谁最小,最小的当作联通组件。
以下图说明,就是顶点 (7L, "Grace") 迭代一步去寻找最小顶点做联通组件,只能迭代到顶点 (5L, "Eve") ,没法迭代到 (1L, "Alice") ,这时顶点 (7L, "Grace") 就会拿自身与顶点 (5L, "Eve") 比较,发现 5L 更小,就会用 5L 当作自己的联通组件做关联,即 (7,5)。
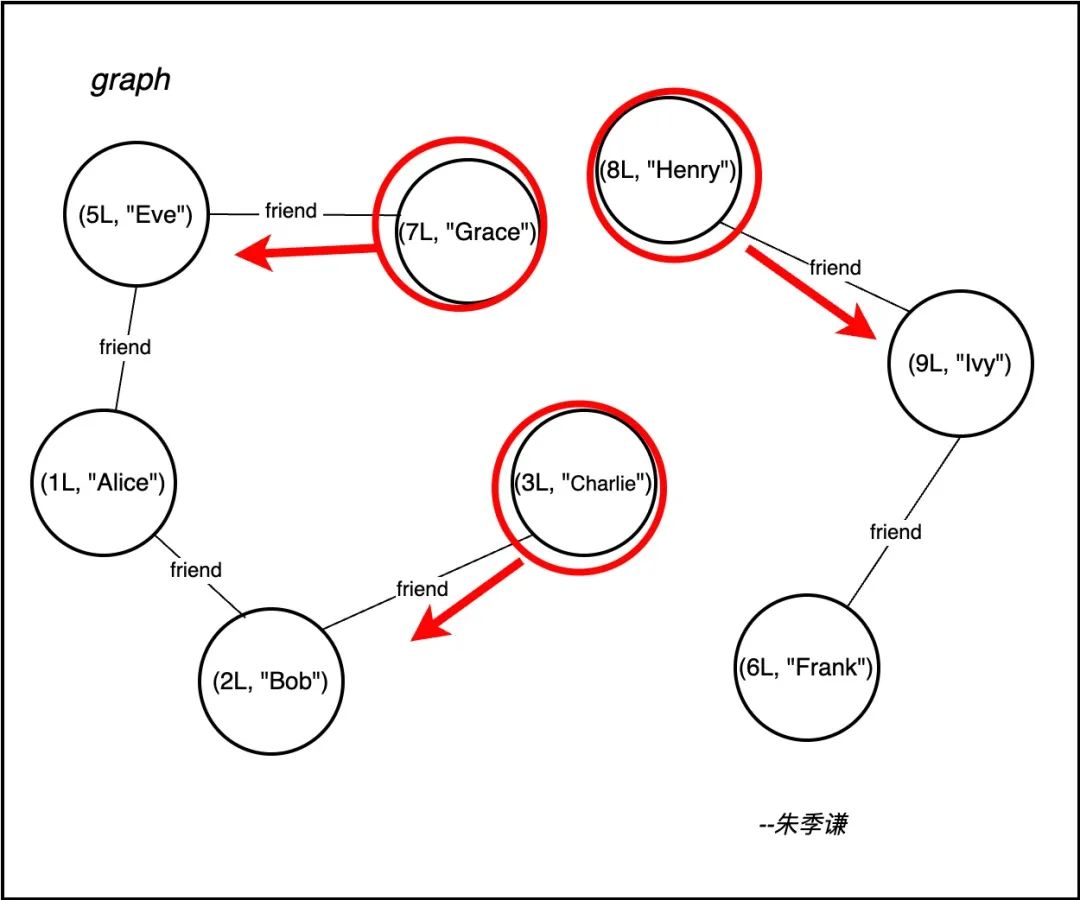
当然,实际底层的源码实现,并非是通过迭代多少步去寻找最小顶点,它的实现方式更精妙,站在原地就可以收集到所能迭代最大次数范围内的最小顶点。
如果 connectedComponents 没有设置参数,就会默认最大迭代次数是 Int.MaxValue,2 的 31 次方 - 1即 2,147,483,647。
在实际业务当中,可以通过设置参数来避免在过大规模的子图里做耗时过长的迭代操作
接下来,就可以通过联通组件做分组,将具有共同联通组件的顶点分组到一块,这样就知道哪些顶点属于同一子图了。
`val cc = graph.connectedComponents()
val group = cc.vertices.map{
case (verticeId, minId) => (minId, verticeId)
}.groupByKey()
group.foreach(println)
打印结果——
(1,CompactBuffer(1, 2, 3, 5, 7))
(6,CompactBuffer(8, 9, 6))`
基于这个函数,就可以得到哪些顶点在一张关系网里了。
connectedComponents 源码解析
先来看一下 connectedComponents 函数源码,在 connectedComponents 单例对象里,可以看到,如果没有传参的话,默认迭代次数是 Int.MaxValue,如果传参的话,就使用参数的 maxIterations 做迭代次数——
`/**
*无参数
*/
def connectedComponents(): Graph[VertexId, ED] = {
ConnectedComponents.run(graph)
}
def run[VD: ClassTag, ED: ClassTag](graph: Graph[VD, ED]): Graph[VertexId, ED] = {
run(graph, Int.MaxValue)
}
/**
*有参数
*/
def connectedComponents(maxIterations: Int): Graph[VertexId, ED] = {
ConnectedComponents.run(graph, maxIterations)
}`
在 run 方法里,主要是做了一些函数和常量的准备工作,然后将这些函数和常量传给单例对象 Pregel 的 apply 方法。apply 是单例对象的特殊方法,就像 Java 类里的构造方法一样,创建对象时可以直接被调用。Pregel(ccGraph, initialMessage,maxIterations, EdgeDirection.Either)(……) 最后调用的就是 Pregel 里的 apply 方法。
` } else if (edge.srcAttr > edge.dstAttr) {
//保存(源顶点 ID,目标顶点 ID)
Iterator((edge.srcId, edge.dstAttr))
} else {
//如果两个顶点属性相同,说明已经在同一个子网里,不需要处理
Iterator.empty
}
}
//step3 设置一个初始最大值,用于在初始化阶段,比较每个顶点的属性,这样顶点属性值在最初阶段就相当是最小顶点
val initialMessage = Long.MaxValue
//step4 将上面设置的常量和函数当作参数传给 Pregel,其中 EdgeDirection.Either 表示处理包括出度和入度的顶点。
val pregelGraph = Pregel(ccGraph, initialMessage,
maxIterations, EdgeDirection.Either)(
//将最初顶点的属性 attr 与 initialMessage 比较,相当是子图的 0 次迭代寻找最小顶点
vprog = (id, attr, msg) => math.min(attr, msg),
//上面定义的 sendMessage 方法
sendMsg = sendMessage,
//处理各个顶点收到的消息,然后将最小的顶点保存
mergeMsg = (a, b) => math.min(a, b))
ccGraph.unpersist()
pregelGraph
}`
step1 初始化图,将各顶点 ID 设置为顶点属性,图顶点结构
`(vid,vid)——
val ccGraph = graph.mapVertices { case (vid, _) => vid }`
写一个简单的代码验证一下即可知道得到的 ccGraph 处理后顶点是否为(vid,vid)结构了。
`// 创建边 RDD
val edges = ss.sparkContext.parallelize(Seq(
Edge(5L, 7L, "friend"),
Edge(5L, 1L, "friend"),
Edge(1L, 2L, "friend"),
Edge(2L, 3L, "friend"),
Edge(6L, 9L, "friend"),
Edge(9L, 8L, "friend")
))
//创建一个 Graph 图
val graph = Graph(vertices, edges, null)
graph.mapVertices{case (vid,_) => vid}.vertices.foreach(println)
打印结果——
(2,2)
(5,5)
(3,3)
(6,6)
(7,7)
(8,8)
(1,1)
(9,9)`
可见,ccGraph 的图顶点已经被处理成(vid,vid),即(顶点 ID, 顶点属性),方便用于在 sendMessage 方法做属性判断处理。
step2 sendMessage 处理图里的每一个三元组边对象
前面处理的 ccGraph 顶点数据变成(顶点 id, 顶点属性)就是为了放在这里做处理,这里的 if (edge.srcAttr < edge.dstAttr) 相当是 if (edge.srcId < edge.dstId)。
这个方法是基于边的三元组做处理,将同一边的源顶点和目标顶点比较,筛选出两个顶点最小的顶点,然后针对最大的顶点,保留(最大顶点,最小顶点属性)这样的数据。
`def sendMessage(edge: EdgeTriplet[VertexId, ED]): Iterator[(VertexId, VertexId)] = {
//如果源顶点属性小于目标顶点属性
if (edge.srcAttr < edge.dstAttr) {
//保存(目标顶点 ID,源顶点属性),这里的源顶点属性等于源顶点 ID,其实保存的是(目标顶点ID,源顶点 ID)
Iterator((edge.dstId, edge.srcAttr))
//如果源顶点属性大于目标顶点属性
} else if (edge.srcAttr > edge.dstAttr) {
//保存(源顶点 ID,目标顶点 ID)
Iterator((edge.srcId, edge.dstAttr))
} else {
//如果两个顶点属性相同,说明已经在同一个子网里,不需要处理
Iterator.empty
}
}`
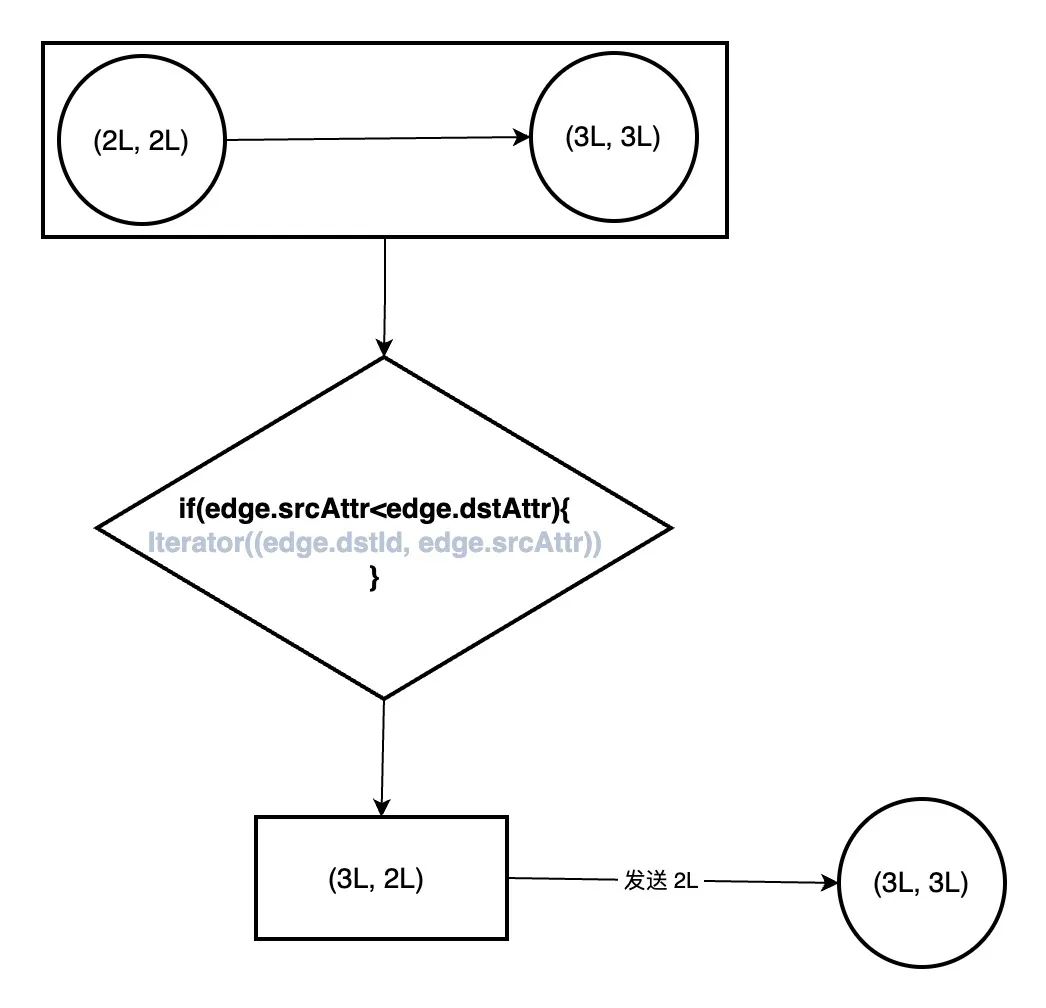
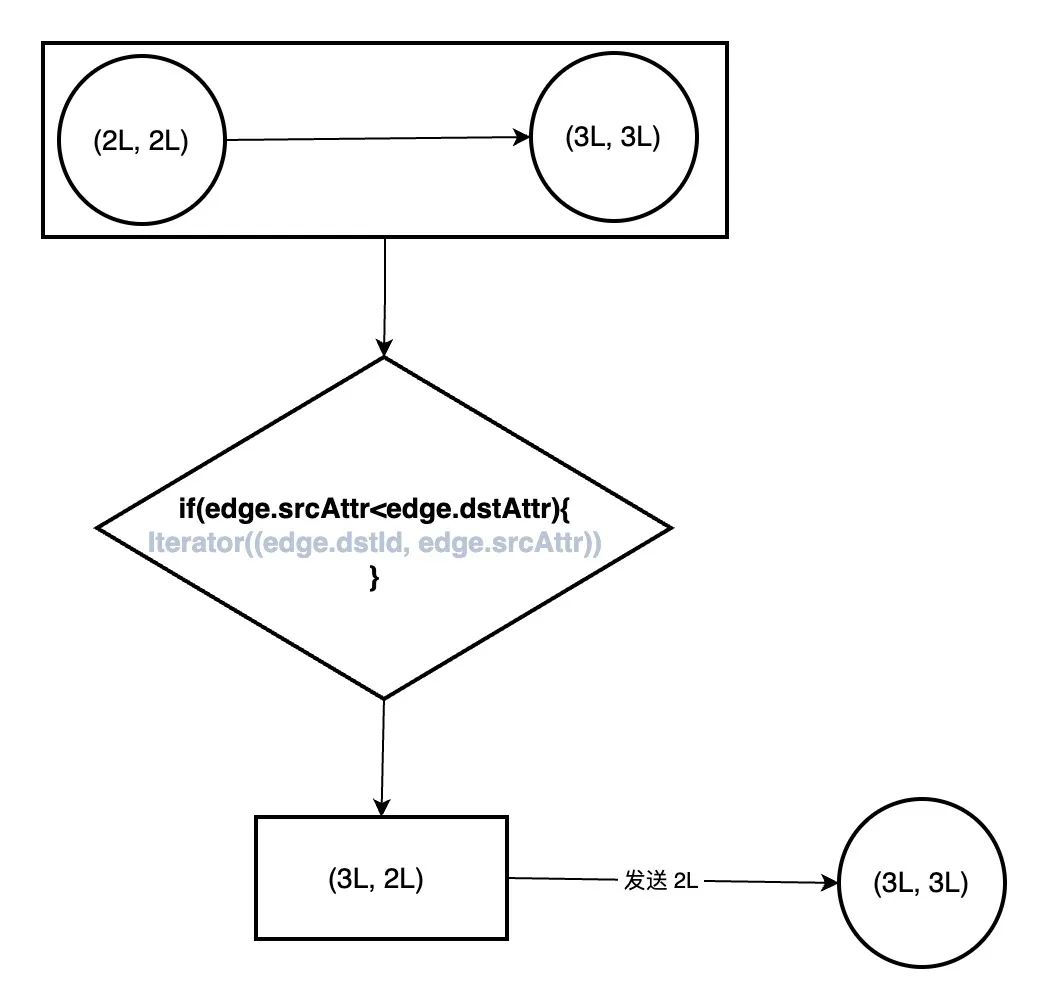
这个方法的作用,就是找出同一条边上哪个顶点最小,例如下图中,2L 比 3L 小,那么 2L 是这条边上最小的顶点,将以最大点关联最小点的方式 (edge.dstId, edge.srcAttr) 即 (3L, 2L) 保存下来。最后会将 (3L, 2L) 中的 _.2 也就是 2L 发送给顶点 (3L, 3L),而顶点 (3L, 3L) 后续需要做的事情是,是将这一轮收到的消息即最小顶点 2L 与现在的属性 3L 值通过 math.min(a, b) 做比较,保留最小顶点当作属性值,即变成了 (3L, 2L)。
可见,在子图里,每一轮迭代后,各个顶点的属性值都可能会被更新接收到的最小顶点值,这就是联通组件迭代的精妙。
这个方法会在后面的 Pregel 对象里用到。
step3 设置一个初始最大值,用于比较后初始化每个顶点最初的属性值
val initialMessage = Long.MaxValue 需要与 vprog = (id, attr, msg) => math.min(attr, msg) 结合来看,相当在 0 次迭代时,将顶点 (id, attr) 的属性值与 initialMessage 做比较,理论上,肯定是 attr 比较小,就意味着初始化时,顶点关联的最小顶点就是 attr,在这里,就相当关联的最小顶点是它本身,相当于子图做了 0 次迭代处理。
step4 执行 Pregel 的构造函数 apply 方法
可以看到,前面创建的 ccGraph,initialMessage,maxIterations(最大迭代次数),EdgeDirection.Either 都当作参数传给了 Pregel。
val pregelGraph = Pregel(ccGraph, initialMessage, maxIterations, EdgeDirection.Either)( //将最初顶点的属性 attr 与 initialMessage 比较,相当是子图的 0 次迭代寻找最小顶点 vprog = (id, attr, msg) => math.min(attr, msg), //上面定义的 sendMessage 方法 sendMsg = sendMessage, //处理各个顶点收到的消息,然后将最小的顶点保存 mergeMsg = (a, b) => math.min(a, b)) 该 Pregel 对象底层主要就是对一系列的三元组边的源顶点和目标顶点做比较,将两顶点最小的顶点值发送给该条边最大的顶点,最大的顶点收到消息后,会比较当前属性与收到的最小顶点值比较,然后保留最小值。这样,每一轮迭代,可能关联的属性值都会一直变化,不断保留历史最小顶点值,直到迭代完成。最后,就可以实现通过 connectedComponents 得到每个顶点都关联到最小顶点的数据。
Pregel 源码解析
Pregel 是一个图处理模型和计算框架,核心思想是将一系列顶点之间的消息做传递和状态更新操作,并以迭代的方式进行计算。让我们继续深入看一下它的底层实现。
以下是保留主要核心代码的函数——
`def apply[VD: ClassTag, ED: ClassTag, A: ClassTag]
(graph: Graph[VD, ED],
initialMsg: A,
maxIterations: Int = Int.MaxValue,
activeDirection: EdgeDirection = EdgeDirection.Either)
(vprog: (VertexId, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED] =
{
......
//step1
var g = graph.mapVertices((vid, vdata) => vprog(vid, vdata, initialMsg))
......
//step2
var messages = GraphXUtils.mapReduceTriplets(g, sendMsg, mergeMsg)
......
//step3
var activeMessages = messages.count()
var prevG: Graph[VD, ED] = null
var i = 0
//step4
while (activeMessages > 0 && i < maxIterations) {
prevG = g
g = g.joinVertices(messages)(vprog)
val oldMessages = messages
messages = GraphXUtils.mapReduceTriplets(
g, sendMsg, mergeMsg, Some((oldMessages, activeDirection)))
activeMessages = messages.count()
i += 1
}
g
}`
这行 var g = graph.mapVertices((vid, vdata) => vprog(vid, vdata, initialMsg)) 代码,需要联系到前面传过来的参数,它的真实面目其实是这样的——
`var g = graph.mapVertices((vid, vdata) => {
(id, attr, initialMsg) => math.min(attr, initialMsg)
})`
也就是前面 step3 里提到的,这里相当做了 0 次迭代,将 attr 当作顶点 ID 关联的最小顶点,初始化后,attr 其实是顶点 ID 本身。
var messages = GraphXUtils.mapReduceTriplets(g, sendMsg, mergeMsg) 这行代码中,主要定义了一个函数 sendMsg 和调用了 aggregateMessagesWithActiveSet 方法。
`private[graphx] def mapReduceTriplets[VD: ClassTag, ED: ClassTag, A: ClassTag](
g: Graph[VD, ED],
mapFunc: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
reduceFunc: (A, A) => A,
activeSetOpt: Option[(VertexRDD[_], EdgeDirection)] = None): VertexRDD[A] = {
def sendMsg(ctx: EdgeContext[VD, ED, A]) {
mapFunc(ctx.toEdgeTriplet).foreach { kv =>
val id = kv._1
val msg = kv._2
if (id == ctx.srcId) {
ctx.sendToSrc(msg)
} else {
assert(id == ctx.dstId)
ctx.sendToDst(msg)
}
}
}
g.aggregateMessagesWithActiveSet(
sendMsg, reduceFunc, TripletFields.All, activeSetOpt)
}`
函数 sendMsg 里需要看懂一点是,这里的 mapFunc(ctx.toEdgeTriplet) 正是调用了前面定义的 connectedComponents 里的 sendMessage 方法,因此,这个方法恢复原样,是这样的——
`def sendMsg(ctx: EdgeContext[VD, ED, A]) {
(ctx.toEdgeTriplet => {
case edge =>
if (edge.srcAttr < edge.dstAttr) {
Iterator((edge.dstId, edge.srcAttr))
} else if (edge.srcAttr > edge.dstAttr) {
Iterator((edge.srcId, edge.dstAttr))
} else {
Iterator.empty
}
}).foreach { kv =>
val id = kv._1
val msg = kv._2
if (id == ctx.srcId) {
ctx.sendToSrc(msg)
} else {
assert(id == ctx.dstId)
ctx.sendToDst(msg)
}
}
}`
这个方法的作用,就是找出同一条边上哪个顶点最小,例如下图中,2L 比 3L 小,那么 2L 是这条边上最小的顶点,将以最大点关联最小点的方式 (edge.dstId, edge.srcAttr) 即 (3L, 2L) 保存下来。最后会将 (3L, 2L) 中的 _.2 也就是 2L 发送给顶点 (3L, 3L),而顶点 (3L, 3L) 后续需要做的事情是,是将这一轮收到的消息即最小顶点 2L 与现在的属性 3L 值通过 math.min(a, b) 做比较,保留最小顶点当作属性值,即变成了 (3L, 2L)。
剩下 aggregateMessagesWithActiveSet 就是做聚合了,sendMsg 就是上面的获取最小顶点后发送给顶点的操作,reduceFunc 对应的是 mergeMsg = (a, b) => math.min(a, b)),保留历史最小顶点当作该顶点属性。
`g.aggregateMessagesWithActiveSet(
sendMsg, reduceFunc, TripletFields.All, activeSetOpt)`
最后这个 while 遍历,如果设置了迭代次数,迭代次数就会传至给 maxIterations,activeMessages 表示还有多少顶点需要处理。
`while (activeMessages > 0 && i < maxIterations) {
prevG = g
g = g.joinVertices(messages)(vprog)
val oldMessages = messages
messages = GraphXUtils.mapReduceTriplets(
g, sendMsg, mergeMsg, Some((oldMessages, activeDirection)))
activeMessages = messages.count()
i += 1
}`
这个方法,就是不断做迭代,不断更新各个顶点属性对应的最小顶点,直到迭代出子图里的最小顶点。
很精妙的一点设计是,每个顶点只需要不断迭代,以三元组边为维度,互相将最小顶点发送给属性值(顶点保留的上一轮最小顶点所做的属性)较大的顶点,顶点只需要保留收到的消息里最小的顶点更新为属性值即可。